<!doctype html public "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html>
<!-- Generated from TeX source by tex2page, v 4o4,
(c) Dorai Sitaram, http://www.cs.rice.edu/~dorai/tex2page -->
<head>
<title>
Revised^5 Report on the Algorithmic Language Scheme
</title>
<link rel="stylesheet" type="text/css" href="r5rs-Z-C.css" title=default>
<meta name=robots content="noindex,follow">
</head>
<body>
<p><div class=navigation>[Go to <span><a href="r5rs.html">first</a>, <a href="r5rs-Z-H-12.html">previous</a></span><span>, <a href="r5rs-Z-H-14.html">next</a></span> page<span>; </span><span><a href="r5rs-Z-H-2.html#%_toc_start">contents</a></span><span><span>; </span><a href="r5rs-Z-H-15.html#%_index_start">index</a></span>]</div><p>
<a name="%_chap_Temp_9"></a>
<h1 class=chapter>
<div class=chapterheading> </div><p>
<a href="r5rs-Z-H-2.html#%_toc_%_chap_Temp_9">Example</a></h1><p>
<p><p>
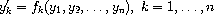
<tt>Integrate-system</tt> integrates the system
<p><div align=left><img src="r5rs-Z-G-63.gif" border="0"></div><p>
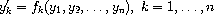
of differential equations with the method of Runge-Kutta.<p>
The parameter <tt>system-derivative</tt> is a function that takes a system
state (a vector of values for the state variables <em>y</em><sub>1</sub>, <tt>...</tt>, <em>y</em><sub><em>n</em></sub>)
and produces a system derivative (the values <em>y</em><sub>1</sub><sup>/</sup>, <tt>...</tt>,
<em>y</em><sub><em>n</em></sub><sup>/</sup>). The parameter <tt>initial-state</tt> provides an initial
system state, and <tt>h</tt> is an initial guess for the length of the
integration step.<p>
The value returned by <tt>integrate-system</tt> is an infinite stream of
system states.<p>
<tt><p>(define integrate-system<br>
(lambda (system-derivative initial-state h)<br>
(let ((next (runge-kutta-4 system-derivative h)))<br>
(letrec ((states<br>
(cons initial-state<br>
(delay (map-streams next<br>
states)))))<br>
states))))<p></tt><p>
<tt>Runge-Kutta-4</tt> takes a function, <tt>f</tt>, that produces a
system derivative from a system state. <tt>Runge-Kutta-4</tt>
produces a function that takes a system state and
produces a new system state.<p>
<tt><p>(define runge-kutta-4<br>
(lambda (f h)<br>
(let ((*h (scale-vector h))<br>
(*2 (scale-vector 2))<br>
(*1/2 (scale-vector (/ 1 2)))<br>
(*1/6 (scale-vector (/ 1 6))))<br>
(lambda (y)<br>
;; y is a system state<br>
(let* ((k0 (*h (f y)))<br>
(k1 (*h (f (add-vectors y (*1/2 k0)))))<br>
(k2 (*h (f (add-vectors y (*1/2 k1)))))<br>
(k3 (*h (f (add-vectors y k2)))))<br>
(add-vectors y<br>
(*1/6 (add-vectors k0<br>
(*2 k1)<br>
(*2 k2)<br>
k3))))))))<br>
<br>
(define elementwise<br>
(lambda (f)<br>
(lambda vectors<br>
(generate-vector<br>
(vector-length (car vectors))<br>
(lambda (i)<br>
(apply f<br>
(map (lambda (v) (vector-ref v i))<br>
vectors)))))))<br>
<br>
(define generate-vector<br>
(lambda (size proc)<br>
(let ((ans (make-vector size)))<br>
(letrec ((loop<br>
(lambda (i)<br>
(cond ((= i size) ans)<br>
(else<br>
(vector-set! ans i (proc i))<br>
(loop (+ i 1)))))))<br>
(loop 0)))))<br>
<br>
(define add-vectors (elementwise +))<br>
<br>
(define scale-vector<br>
(lambda (s)<br>
(elementwise (lambda (x) (* x s)))))<p></tt><p>
<tt>Map-streams</tt> is analogous to <tt>map</tt>: it applies its first
argument (a procedure) to all the elements of its second argument (a
stream).<p>
<tt><p>(define map-streams<br>
(lambda (f s)<br>
(cons (f (head s))<br>
(delay (map-streams f (tail s))))))<p></tt><p>
Infinite streams are implemented as pairs whose car holds the first
element of the stream and whose cdr holds a promise to deliver the rest
of the stream.<p>
<tt><p>(define head car)<br>
(define tail<br>
(lambda (stream) (force (cdr stream))))<p></tt><p>
<p><br><p><br><p>The following illustrates the use of <tt>integrate-system</tt> in
integrating the system
<p><div align=left><img src="r5rs-Z-G-64.gif" border="0"></div><p><p><div align=left><img src="r5rs-Z-G-65.gif" border="0"></div><p>
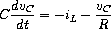
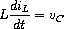
which models a damped oscillator.<p>
<tt><p>(define damped-oscillator<br>
(lambda (R L C)<br>
(lambda (state)<br>
(let ((Vc (vector-ref state 0))<br>
(Il (vector-ref state 1)))<br>
(vector (- 0 (+ (/ Vc (* R C)) (/ Il C)))<br>
(/ Vc L))))))<br>
<br>
(define the-states<br>
(integrate-system<br>
(damped-oscillator 10000 1000 .001)<br>
'#(1 0)<br>
.01))<p></tt><p>
<p>
<p>
<p><div class=navigation>[Go to <span><a href="r5rs.html">first</a>, <a href="r5rs-Z-H-12.html">previous</a></span><span>, <a href="r5rs-Z-H-14.html">next</a></span> page<span>; </span><span><a href="r5rs-Z-H-2.html#%_toc_start">contents</a></span><span><span>; </span><a href="r5rs-Z-H-15.html#%_index_start">index</a></span>]</div><p>
</body>
</html>